Optics Overview
Optical Spectrum:
The field of optics began with descriptions of propagating energy that was visible to the human eye. Basic observations of directionality, color, and intensity were made. The effect of materials were used to create mirrors, lenses, and windows. Most early applications involved vision or lighting. For example, a lens (as shown in 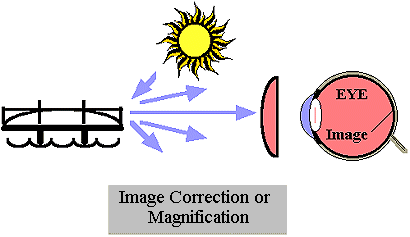 ) can improve image quality correcting faulty vision or magnify an image improving resolution. Prisms were shown to separate light into its component colors. Later studies extended the observations to propagating energy that was not visible. Optical radiation, whether visible or nonvisible, interacts with materials in similar ways. For instance, the physical mechanisms behind many optical sources are electronic and molecular transitions and the methods of beam control often depend on reflection and refraction from interfaces. Hence, the branch of physics known as optics includes all light, i.e. ultraviolet (UV), visible, and infrared (IR) categories.
) can improve image quality correcting faulty vision or magnify an image improving resolution. Prisms were shown to separate light into its component colors. Later studies extended the observations to propagating energy that was not visible. Optical radiation, whether visible or nonvisible, interacts with materials in similar ways. For instance, the physical mechanisms behind many optical sources are electronic and molecular transitions and the methods of beam control often depend on reflection and refraction from interfaces. Hence, the branch of physics known as optics includes all light, i.e. ultraviolet (UV), visible, and infrared (IR) categories.
Light may analyzed using ray, wave, and quantum descriptions. The ray description is the least general and the least complex mathematically. The quantum description is the most general and the most complex. A wave-based analysis is quite adequate for most engineering applications and many scientific purposes. Notable exceptions include some cases of emission and absorption of light. In particular, photoelectric emission led scientists to introduce the concept of photons which was part of the development of the quantum mechanics. Also, the operation of laser diodes and photodiodes can only be explained using a quantum description of semiconductors and light.
The wave-based description linked optical radiation to radio waves, shortwaves, and microwaves. The quantum description linked optical radiation to high-energy particles such as x-rays. The resulting electromagnetic spectrum (see 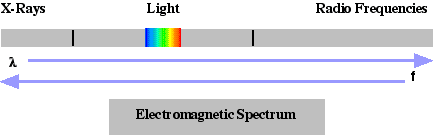 ) characterized the movement of energy by wavelength in vacuum l, frequency f, or quantum energy Eq. Wavelength (as defined in a vacuum) and frequency are related by l f = c where c is the speed of light. The quantum energy of a photon, or optical energy packet, is Eq = hf where h is Planck’s constant. (See the Units section for values.) In the visible spectral band, each wavelength, or energy, gives a distinct color. Chromatic Response (in order of increasing wavelength) are Violet, Blue, Green, Yellow, Orange, and Red. A comparison of the parameters and spectrum categories are given.
) characterized the movement of energy by wavelength in vacuum l, frequency f, or quantum energy Eq. Wavelength (as defined in a vacuum) and frequency are related by l f = c where c is the speed of light. The quantum energy of a photon, or optical energy packet, is Eq = hf where h is Planck’s constant. (See the Units section for values.) In the visible spectral band, each wavelength, or energy, gives a distinct color. Chromatic Response (in order of increasing wavelength) are Violet, Blue, Green, Yellow, Orange, and Red. A comparison of the parameters and spectrum categories are given.
Spectrum | Wavelengths | Frequency | Quantum Energy |
| Microwaves | 105 nm | 2.998 x 1012 Hz | 1.240 x 10-02 eV |
| IR/Visible | 700 nm | 4.283 x 1014 Hz | 1.771 eV |
| Visible/UV | 450 nm | 6.662 x 1014 Hz | 2.755eV |
| X-rays | 1 nm | 2.998 x 1017 Hz | 1.240 x 103 eV |
(see  )
)
Radio frequencies exhibit wave-like behavior primarily since the wavelengths are large and the quantum energies are extremely small. X-rays exhibit largely quantum particle-like behavior since the wavelengths are extremely small and the energy packets are large. Light is unusual in that it readily displays both wave-like and quantum behavior. Optical wavelengths include wavelengths between about 1 nm and 105 nm. (The internal band divisions are approximate in that they are defined by the response of the typical human eye.)
Light Bands | Lower Wavelength Limit | Upper Wavelength Limit |
| Infrared (IR) | about 700 nm | about 105 nm |
| Visible | about 450 nm | about 700 nm |
| Ultraviolet (UV) | about 1 nm | about 450 nm |
(See  )
)
Optical Phenomena:
The application of optical radiation has three considerations — propagation, sources, and detectors. It may be described as a ray with a direction of energy flow, a wave with time- and space-dependent coupling of electric and magnetic vector fields, and a photon with a discrete energy. The ray description of light is usually limited to simple analysis of propagation and to the effects of optical elements based on interfaces, e.g. lenses and mirrors. The electromagnetic description is generally adequate for a wide range of analysis for general propagation, emission, and absorption. The quantum description is mostly used for analysis of light-material interactions, especially semiconductor interactions. It is required for lasers and most detectors. The analysis of optical phenomena depends on the situation and accuracy required.
Types of Optical Analysis
Ray Optics - a geometric representation of the behavior of light (also called geometrical optics) which corresponds to the limiting case of l Æ 0.
Electromagnetic (EM) Optics - or physical optics, an electromagnetics representation of the behavior of light using Maxwell’s equations (limiting case as photon number approach ƒ).
Quantum Optics - the most general representation of the behavior of light in terms of photons, i.e. radiant energy packets, using quantum mechanics.
The characteristics of light may be changed as it propagates through medium or as it falls on surfaces (interfaces between media).  shows a icon-based diagram of a simple optical system with a propagation path through two lenses and an optical fiber wave guide, an incandescent light source, and a human detector. The lenses change the direction of the light so that it is collected by the optical fiber and then the eye. The fiber constrains the propagation path. In general, propagation changes may be active in which the properties of the media depend on an external parameter such as an external field. Passive changes depend on properties inherent to the media itself. The changes include variation in propagation direction, reorientation of polarization (wave vector) state, energy loss, and energy gain.
shows a icon-based diagram of a simple optical system with a propagation path through two lenses and an optical fiber wave guide, an incandescent light source, and a human detector. The lenses change the direction of the light so that it is collected by the optical fiber and then the eye. The fiber constrains the propagation path. In general, propagation changes may be active in which the properties of the media depend on an external parameter such as an external field. Passive changes depend on properties inherent to the media itself. The changes include variation in propagation direction, reorientation of polarization (wave vector) state, energy loss, and energy gain.
Changes in the Direction of Light
Reflection - the specular (mirror-like) return of light as it is incident on a different medium.
Refraction - the bending of obliquely-incident light as it passes into a different medium.
Diffraction - deviations from rectilinear paths not due to reflection or refraction.
Scatter - change in the spatial distribution of a wave from interaction with a surface or heterogeneous medium. (Usually applied to interaction with microirregulaities in a surface or medium that are described statistically.)
Other Passive Changes
Interference - systematic attenuation and reinforcement of overlapping waves. (This effect does not require a medium and may occur in vacuum.)
Retardation — the reduction in phase velocity while propagating in a medium.
Dispersion — the separation of wave components due to variation in velocity with wavelength l.
Changes in the Irradiance of Light
Absorption - loss due to energy conversion as light passes through a material (this effect is usually passive, but may be active).
Amplification - gain; increase in the irradiance of a wave as it transverses media without significant distortion of the wavefront. (The associated medium is called an active medium.)
Emission - conversion of energy into light.
Other Active Changes
Electro-optic (EO) - the technology which uses applied low-frequency electric fields to control optical radiation. (It can also refer to devices which convert electrical signals to optical signal and vice versa such as laser diodes and photodiodes).
Acousto-optic (AO) - the technology which employs the interaction between sound waves and optical radiation typically to control the direction of propagation.
Magneto-optic - the technology which uses applied magnetic fields to control optical radiation.
Nonlinear optics (NL) - the technology in which optical radiation has complex interactions with material and can produce amplitude-dependent behavior, can alter its frequency, etc.
These optical phenomena are exploited to create lenses, wave guides, polarizers, sources, photodetectors, and other optical elements. Common materials for optical elements include glassy dielectrics, crystals, metals, and semiconductors. Surface irregularities and bulk inhomogeneities as small as the wavelength of light may significantly effect the propagation.
Many types of sources and detectors exist. 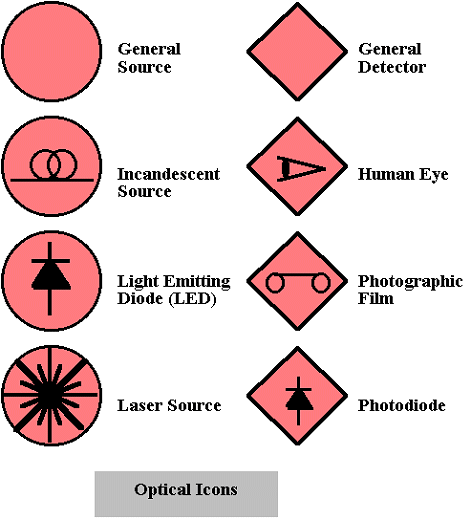 shows icons for some of the common devices which emit or detect light.
shows icons for some of the common devices which emit or detect light.
Light is produced by many methods. Key properties include spectrum, coherence, and directionality and greatly effect optical interference and energy concentration. The spectrum refers to the range of wavelengths emitted. The coherence is the phase relation between various parts of the light. The directionality relates to how the energy in light spreads with propagation.
Types of Sources
Incandescent Lamp - Light is emitted from a heated metallic wire in a vacuum. The wire has a high resistance and is heated by a current. The emission spectrum is extremely broad extending from the infrared into the visible spectrum.
Arc Lamp - Light is emitted from an electric arc between electrodes in a gaseous environment. The wavelengths emitted have a relatively narrow spectral range and are different for different materials.
Light Emitting Diode (LED) - Light is emitted due to quantum transitions in a semiconductor structure and are consequently centered around a characteristic wavelength. The range of wavelengths emitted are relatively narrow, but they have poor coherence.
Lasers (Light Amplification by Stimulated Emission of Radiation) - Light is emitted due to quantum transitions in gases, liquids, or solids. These sources are characterized by high coherence and directionality over an extremely narrow spectrum. 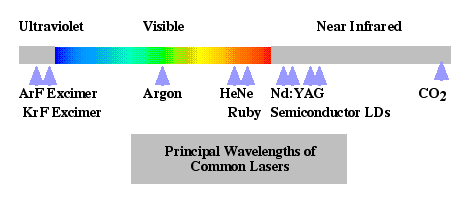 shows the emission wavelengths of various laser types. Technically useful lasers include CO2 gas lasers operating at 10,600 nm, Nd:YAG crystalline lasers operating at 1064 nm, HeNe gas lasers operating at 633 nm, and laser diodes (LDs) operating at a variety of wavelengths including the important fiber optic wavelengths of 1300 nm and 1550 nm. Laser diodes will produce an optical irradiance proportional to the electrical current.
shows the emission wavelengths of various laser types. Technically useful lasers include CO2 gas lasers operating at 10,600 nm, Nd:YAG crystalline lasers operating at 1064 nm, HeNe gas lasers operating at 633 nm, and laser diodes (LDs) operating at a variety of wavelengths including the important fiber optic wavelengths of 1300 nm and 1550 nm. Laser diodes will produce an optical irradiance proportional to the electrical current.
Light irradiance must be detected or monitored in almost all optical applications. The eye is a common detector. As shown in 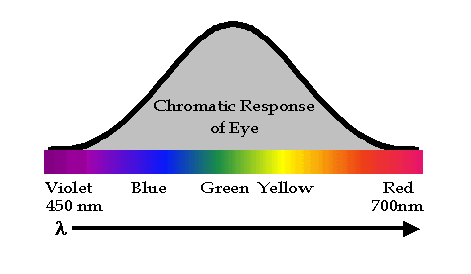 , the sensitivity of the eye peaks in the "green" portion of the visible spectrum around a wavelength of 500 nm and falls off toward the edges of the visible spectrum. The color response of the eye is determined by wavelength. A given wavelength will be perceived as a single color, however, the same sensation of color can be produced by a combination of wavelengths. Light measurement for illumination is weighted by the spectral or chromatic response of the "typical" young human eye (and thus only applies to the visible spectrum) and is called photometry with units of luminous intensity being the candela. The measurements of light in the context of this course will be independent of the human eye response and is called radiometry with units of luminous intensity being watts per steradian. A variety of man-made detectors exist for different optical applications.
, the sensitivity of the eye peaks in the "green" portion of the visible spectrum around a wavelength of 500 nm and falls off toward the edges of the visible spectrum. The color response of the eye is determined by wavelength. A given wavelength will be perceived as a single color, however, the same sensation of color can be produced by a combination of wavelengths. Light measurement for illumination is weighted by the spectral or chromatic response of the "typical" young human eye (and thus only applies to the visible spectrum) and is called photometry with units of luminous intensity being the candela. The measurements of light in the context of this course will be independent of the human eye response and is called radiometry with units of luminous intensity being watts per steradian. A variety of man-made detectors exist for different optical applications.
Types of Detectors
Photographic Film - Light produces a chemical change in an emulsion that is fixed in a development process. A fine spatial distribution can be recorded for image or information storage.
Thermoelectric Materials - Absorbed light produces a temperature change that is detected through a resistance, voltage, or current. Examples include bolometers, thermocouples, pyroelectric detectors. These devices are often used to measure infrared radiation and to measure high power laser beams.
Semiconductor Structures - Incident photons are converted by semiconductor structures into usable electrons. Solar cells convert light to electrical power. Common devices for imaging and information detection are CCDs (charge coupled devices), photodiodes, and avalanche photodiodes. Photodiodes will produce a electrical current proportional to the irradiance of light absorbed. The design of semiconductor photodetectors depends on the wavelength sensitivity of the materials (see 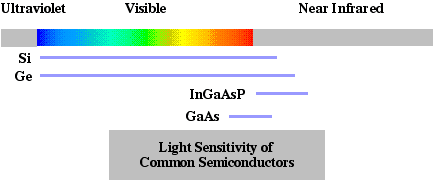 ). For instance, silicon and germanium are sensitive across the visible spectrum and near infrared spectrum. The compound semiconductors InGaAsP and GaAs are sensitive in the upper visible and near infrared. The peak quantum efficiency (electronic conductors generated per incident photon) of about 900 nm in silicon is near its upper cut-off wavelength of 1100 nm. Detectors made of materials such as InGaAsP are optimized for important optical fiber wavelengths of 1300 nm and 1550 nm.
). For instance, silicon and germanium are sensitive across the visible spectrum and near infrared spectrum. The compound semiconductors InGaAsP and GaAs are sensitive in the upper visible and near infrared. The peak quantum efficiency (electronic conductors generated per incident photon) of about 900 nm in silicon is near its upper cut-off wavelength of 1100 nm. Detectors made of materials such as InGaAsP are optimized for important optical fiber wavelengths of 1300 nm and 1550 nm.
Electromagnetic Waves:
An electromagnetic (EM) wave consists of a coupled vector electric field and magnetic field. Both field quantities vary in time t and spatial coordinates (x,y,z) and describe the propagation of energy. A general wave may consist of various wavelengths, directions, amplitudes, etc. However, each wavelength is independent in most situations and may be considered separately. Furthermore a monochromatic, or single wavelength, wave may separated into simple component parts. A set of "plane" waves is a common decomposition. These waves have perfect coherence and a single direction of propagation. They are useful mathematical representations for light from lasers and to some extent from LEDs.
A wave function is one in which a quantity U travels in a given direction with a given velocity. For instance, the wave U(z,t) = f(z — vt) depends only on (z — vt) as shown in 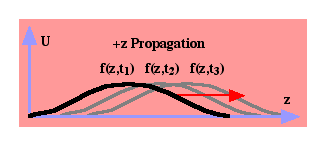 . A given point on the function f(•) will move in the positive z-direction with a velocity v. Note that the argument of f(•) is zero for position z=0 and time t=0. It is also zero for z=zo and t=zo/v. If the wave were U(z,t) = f(z + vt), each point on the function would travel in the negative z-direction with a velocity v. If U represents the voltage on a telephone line, the wave is a scalar. Voltage has no direction, but the voltage signal is propagating down the line. If U represents the material displacement caused by a sound wave, the wave is a vector quantity in which the displacement has a vector direction longitudinal with the sound propagation. If U is the displacement of a vibrating spring, the string displacement has a vector direction transverse to the traveling vibration.
. A given point on the function f(•) will move in the positive z-direction with a velocity v. Note that the argument of f(•) is zero for position z=0 and time t=0. It is also zero for z=zo and t=zo/v. If the wave were U(z,t) = f(z + vt), each point on the function would travel in the negative z-direction with a velocity v. If U represents the voltage on a telephone line, the wave is a scalar. Voltage has no direction, but the voltage signal is propagating down the line. If U represents the material displacement caused by a sound wave, the wave is a vector quantity in which the displacement has a vector direction longitudinal with the sound propagation. If U is the displacement of a vibrating spring, the string displacement has a vector direction transverse to the traveling vibration.
An optical plane wave is a transverse wave function existing in three dimensions. The coupled vector electric and magnetic fields are transverse to the direction of energy flow. An ideal plane wave is infinite in extent. Consider sinusoidal plane wave propagation in the +z-direction as shown in 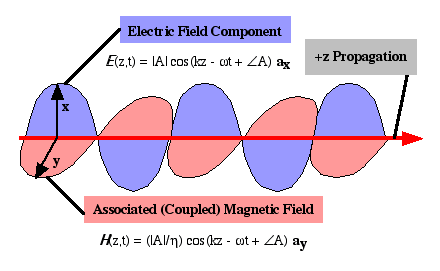 . The vector electric field is
. The vector electric field is
E (z, t) ae = |E| cos(- wt + kz + Q) ae V/m
where ae is in the xy plane (transverse to the +z-propagation direction). The amplitude |E| cannot depend on xy coordinates, but may include gain or loss with dependence on z. The total phase of the wave is (- wt + kz + Q). The parameters are angular velocity w, propagation constant k, and relative phase Q. The wavelength l, frequency f, speed of light c, and phase velocity vp are related as
w = 2¼f = 2¼nvp/l = 2¼c/l,
k = 2¼n/l = 2¼f/vp = 2¼nf/c = wn/c,
lf = c, and lf/n = c/n = vp.
The quantity n is the index of refraction or refractive index and is a dimensionless function of the media of propagation. It is often defined as the ratio n = c/vp.
The physics of the propagation requires that magnetic field be
H (z, t) ae = |H| cos(- wt + kz + Q) ae
where ae ¥ ah = + az (i.e. the magnetic field is tranverse to the electric field and to the propagation direction), and |H| = |E| (n / ho). The ratio of |E| to |H| is the characteristic impedance of the media (ho / n). The quantity ho is the characteristic impedance of vacuum and is a physical constant ho = 376.7 ‡.
Irradiance - Waves represent the propagation of energy and the quantity detected is the energy itself verses direct detection of the field quantities. The total energy in a true plane wave is infinite since the wave is infinite in extent. Irradiance is the power per unit area (W/m2). For a z-propagating plane wave the instantaneous irradiance is
Iinstananeous = |E| |H| cos2 (- wt + kz + Q) = (|E|2 / h) cos2(- wt + kz + Q) W/m2.
The large frequency of optical waves prevents the instantaneous measurement of irradiance. Consequently, irradiance will refer to the time-averaged irradiance I unless specifically stated otherwise. Hence,
I = (1/2) |E| |H| = (|E|2 / 2h).
